线性代数
MIT线性代数课程笔记,向所有想学好线代的同学推荐此课。听GS老爷子课,如饮醇醪。
注:文中的“零”、
多数是指零向量。
矩阵乘法的几种视角
矩阵A(m*n)和B(n*p)相乘,得到m*p的矩阵C。
单个元素
很少用。
的值是A中第 行与B中第 列点乘的结果, 。 列的线性组合
将B看成是
个单独的列向量,C中各列是A中各列的线性组合(C中的每一列都由A乘B中对应列向量得到,B列向量即A中各列的组合方式)。 行的线性组合
与2同理,将A看成是
个单独的行向量,C中各行是B中各行的线性组合(C中的每一行都由A中对应行向量乘B得到)。 单行乘单列
与1相背,取A中一列(m*1),B中一行(1*p),相乘得到一个(m*p)的矩阵。C实际上是A中各列与B中各行乘积之和(第一列乘第一行,加上第二列乘第二行……)。
模块化的视角
将A和B划成小块,乘法和上面的乘法一样。
矩阵有逆的几种理解
(撒盐空中差可拟)奇异(不可逆矩阵)的行列式为0;
(未若柳絮因风起)奇异矩阵各列能够通过线性组合得到0。即能够找到一个不为0的向量
,使得 。
高斯-若尔当消元
对于可逆矩阵A,
为什么A=LU好于EA=U?
假设对于矩阵
转置矩阵
由
对于置换矩阵P,有
求解Ax=0
求解矩阵的零空间(nullspace),通过消元使矩阵成为rref格式,即可得到x的解。例:
矩阵有两个主元,一个自由变元。此时可以写出消元后的方程:
令自由变元
该格式null中正是通过rref化简来求矩阵的零基。
求解Ax=b
有解:有解意味着b必须在A的列空间中,即A中各列的线性组合能得到b。另一个等价的表述是:如果A中各行的线性组合得到零行,那么b中对应的线性组合结果要为0。
求解:知道了如何求解
,再求解 就简单了。因为 可以看成是 ,其中通解 即 解出的零空间向量, 称为 的特解,可以通过设自由变元为0解出。 INFO
特解有无数个,“令自由变元为0”只是因为方便,由
, ,可以令 ,这里的 是 向量,从而消去 快速得到一个 ,其他的特解无非是这个解加上若干倍的 。 解的个数:如果矩阵列满秩
,矩阵又瘦又长,则自由变元的个数为0,此时零空间只有零向量。显然 只有一个解。更多的时候没有解。若行满秩 ,则有 个自由变元,此时必定有多解。若 ,此时矩阵为方阵且为可逆矩阵(因为可以消元为 的格式),有且只有一个解。 秩 矩阵形状 方阵 瘦长 宽短 不确定 rref格式 解的个数 或 0或
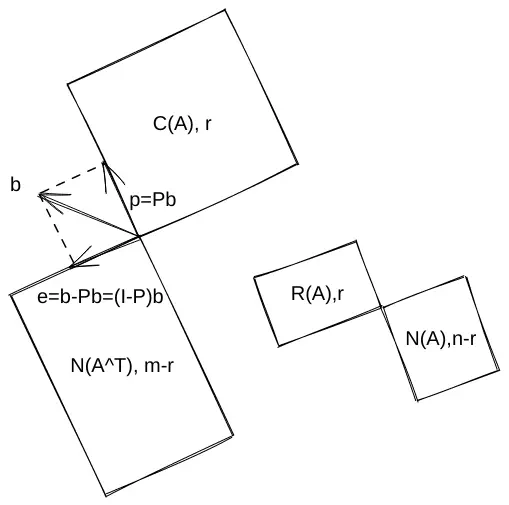
矩阵的四个子空间
| 属于 | 维度 | 基向量的构造 | |
|---|---|---|---|
| 列空间 | 主元所在的列 | ||
| 零空间 | |||
| 行空间 | rref之后剩下的非0行,因为消元过程都是各行的线性组合,得到的结果依然在行空间中 | ||
| 左零空间 | 即 |
应用示例
考虑如下的有向图:
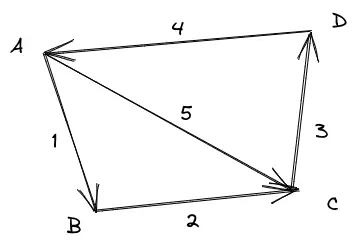
我们用矩阵
- 矩阵
的1、2、5行是线性相关的,实际上它们恰好构成了ABC这个回路; - 矩阵的维度和秩
; - 矩阵的零空间是一维的,
。
考虑
如果
INFO
C是如何与电导产生联系的?为什么这里可以说是欧姆定律的体现?
考虑
这个式子表述的是各个结点出入的电流相等,即基尔霍夫定律。
回路就意味着线性相关,现在可进一步解释回路与秩的关系,
INFO
为什么是
整理上述步骤,把电势方程记为
正交矩阵和投影
正交向量
两个向量正交意味着
投影矩阵
很多时候我们的
下图中,
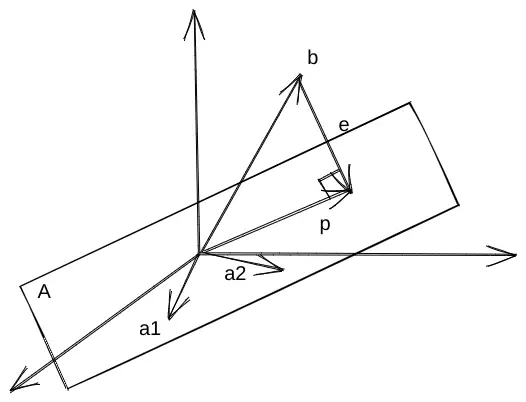
由于
; (一次投影来到列空间内,再次投影保持不动了); - 当
是一维向量的时候, 退化为一个数,因此 可以写成 ; - 如果
在 的列空间中,有 (因为此时 , );如果 ,说明 在 中,有 ,得 。
最小二乘法成立条件
在直线拟合问题中,列出误差
标准正交基
如果矩阵
,若 为方阵, ; - 在投影矩阵的问题中,如果
是 ,那么有 (如果 为方阵,进一步有 ),此时 变为 ,可以立即得到 的解。
正交化方法与A=QR
(格拉姆-施密特正交化方法)对于线性无关的向量组,可以利用投影矩阵计算出对应的一组正交向量,如果这些向量组作为列向量构成矩阵
行列式
行列式的若干性质
; - 如果交换矩阵的行(或列)一次,行列式的值变为其相反数;
; 。 - 如果矩阵有相同行(或列),则行列式的值为0。可以利用性质2,交换后得到的相反数为自身推出;
- 为第
行减去第 行的若干倍,不改变行列式的值(结合3和4可证); - 若存在零行(列),行列式的值为0;
- 三角矩阵或对角矩阵
的行列式等于主元的乘积(对于对角矩阵,可以通过消元变为I,乘数即是主元的积;对于三角矩阵,可以进一步消元得到对角矩阵,这一过程行列式的值不变)。这一性质提供了计算行列式的有效方法,以及 等; - 奇异矩阵的行列式为0;
,同时易知若 可逆,有 ; 。依然通过消元的思想证明,如果 是奇异矩阵显然成立;如果 可逆, 可以消元为 的格式,其中 (因为主元全为1),而 等于 ,同样的有 ,又因为 是上三角矩阵,有 ,得证。
代数余子式和伴随矩阵
以一个
类似的,3阶矩阵可以分解为6项,4阶矩阵可以分解为24项……其思路是固定第
如果对矩阵
行列式的若干应用
矩阵的逆
即证
根据
面积和体积
行列式的值等于向量所确定的图形的面积或体积。例如
特征值与特征向量
矩阵
若
系统地求
以正交矩阵
特征值也可以只有一个,例如
总结了一些性质:
由于
,知转置矩阵与原矩阵有相同的特征值。 若矩阵可逆,等价于说矩阵的特征值均不为0,否则
有非零解, 不只有零向量,还有该解对应的特征向量 了。 特征值之和等于矩阵的迹,特征值之积等于矩阵的行列式。进一步可知矩阵逆的行列式等于该矩阵特征值之积的倒数。
对角化方法
若取
上述讨论的前提是
一阶线性差分方程与矩阵的幂
如果一个差分方程可以用矩阵表达成
随后解出
一阶线性微分方程与矩阵指数
对于微分方程,假设能够表达成
这里的
和前面的 可看成对应的东西。
以一组相互影响的
令
针对这个问题的
- 想要
收敛,需要式子中所有的 ,则 应该小于0。更进一步,如果 是复数,根据欧拉公式, 部分的模为1,则模 ,需要 的实数部分(后面记作 )小于0. - 如果
,其他的 ,则可以达到一个不为0的稳态; - 其他的情况
“blow up”
INFO
后面的习题课上又补充了一个周期性的例子,假设矩阵
特别的,对于2*2的矩阵,想要具有稳定性,要求矩阵的迹小于0(两个特征值相加,结果为负数),同时行列式大于0(两个特征值都为负数,不能一正一负)。
可以看出,解中各个指数函数是互不相干的。原方程组有两个互相耦合的未知函数,而特征值和特征向量的作用是解耦,又称对角化。将
WARNING
这一段没看懂:
这要求我们允许“矩阵指数”的定义,那么
如何理解指数中有矩阵,也就是这里的
由
INFO
另一个常见级数是几何级数。同样可以有矩阵的形式。由
这实际上也是求逆矩阵的好方法,如果
由于
对于二阶微分方程
特征值与特征向量的应用举例
一阶RC电路
一阶RC电路的电容满足
于是
WARNING
一些疑惑,一开始我令
逻辑斯蒂方程
对于简单逻辑斯蒂方程
马尔可夫矩阵
马尔可夫矩阵是这样的一些矩阵:
- 矩阵的所有项均大于等于0;
- 矩阵各列(某些书上是各行)相加为1.
可以推理出马尔可夫矩阵的一些性质:
- 有一个特征值为1。因为矩阵各列相加为1,而
之后该列位于矩阵对角线上的元素为 ,而其余项之和为 ,该项与其余项之和为0,换句话说 在其零空间里, 为奇异矩阵; - 其他的特征值的绝对值均小于1。这使得最后得到的差分方程解的通式中,除了
的那项之外,其他的项在 足够大时都趋向于0。
INFO
在一阶线性差分方程问题中,特征值为1使得
马尔可夫矩阵的性质很容易和概率问题联系到一起。在一个人口迁徙模型中,假如每年有0.1的人口从A地迁徙到B地,有0.2的人口从B地迁徙到A地,则可以用这样一个矩阵刻画:
傅里叶级数
带有标准正交基的投影
假设向量
这个过程可以理解为将向量展开到正交基上面去。为了求出
从本质上来说,傅里叶级数是上述问题(离散情形)在连续情形下的拓延。傅里叶级数将向量的分解拓展到了函数空间,使用相互正交的
如何理解函数的“正交”,也就是点积为0呢?
对于向量来说,
对于
与离散情形的
右边积出来为
对称矩阵
对称矩阵:
所有的特征值都是实数。由
, , ( 可推出 ,而 ,实矩阵 ),有 ,则 , ,从而 。基于这个推理过程,若 是复数矩阵,则 ,可推出“对称”的条件是 。 特征值不同的特征向量之间相互正交,即
,每个对称矩阵都是一些互相垂直的投影矩阵的组合。(主轴定理,特征向量说明主轴的方向,特征值说明主轴的长度。) 主元的符号和特征值的符号一致。这给了我们计算矩阵特征值的良好方式(
的方法对高阶矩阵很困难):首先用消元求出矩阵的主元,这个计算量很小。随后可以将矩阵平移若干个单位,比如7,则矩阵特征值也平移了7,根据新矩阵主元的变化可知原矩阵有多少特征值大于7或小于7。
INFO
习题课上的拓展:什么样的矩阵具有相互正交的特征向量?满足
正定矩阵
正定矩阵是一些要求更严格的对称矩阵:
- 所有主元大于0;
- 所有特征值大于0;
- 行列式大于0,但是这还不够,要求所有顺序子行列式均大于0。这样才有全正的主元和特征值。
如何理解判别式
以2*2矩阵
INFO
通过这些性质,正主元、正特征值、正行列式、平方和、图像向上原点是最小值都联系在一起了。
从微积分的角度说,关于
一些推论:
- 若
是正定矩阵,则 也是正定矩阵; - 若
、 是正定矩阵,则 是正定矩阵(利用判别式); - 对于普通的长方形矩阵
, 是正定矩阵。(依然利用判别式, ,为了排除等于0的情况,要求 只有零向量,即各列线性无关,即列满秩 )。这个式子我们在最小二乘法那里已经见到了,其正是正定矩阵的出处。
相似矩阵
矩阵
相似矩阵具有相同的特征值。由
比较值得注意的是特征值重复的情况,
奇异值分解(SVD)
SVD的思想在于将行空间的一组(标准)正交基
重点是
伪逆
我们已经学过很多矩阵尤其是长方形矩阵是没有逆的,但在投影矩阵、特征值相关内容的学习中注意到了一些事实:对于列满秩m*n矩阵
INFO
如果将
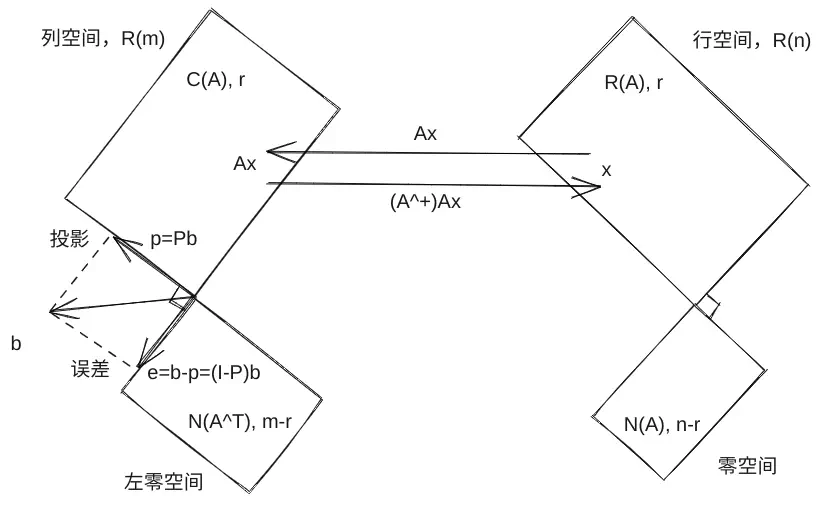
行空间到列空间的映射
我们可以理解正是“零空间”破坏了矩阵的逆,因为如果一个矩阵施加到一个向量上为零,那么没有逆可以还原回去了。对于任意一个向量
行空间和列空间的向量是一一对应的。如果
最后是一幅“Big Picture”: