变换

齐次坐标（Homogeneous coordinates）

如果只用2*2矩阵，会发现无法表示二维平移（move）这种基本变换。因此人们想到了引入一个额外的维度，约定：

1. $\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$表示二维坐标点；
2. $\left[\begin{array}{c}x\\ y\\ 0\end{array}\right]$表示二维向量。

这样平移变换可表示为：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right]=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ z\end{array}\right]$$

点和向量的加减产生了四种运算，进一步说明上面的“约定”不是空穴来风：

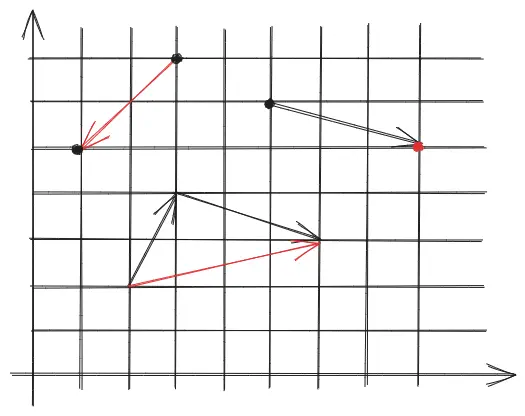
1. 点减去点，运算的结果是向量，含义就是从一个点（减数）指向另一个点（被减数）的向量，如下图左上角$\left[\begin{array}{c}1\\ 5\\ 1\end{array}\right]-\left[\begin{array}{c}3\\ 7\\ 1\end{array}\right]=\left[\begin{array}{c}-2\\ -2\\ 0\end{array}\right]$；
2. 点与向量运算，运算的结果是点，含义其实是从该点走向量到另一个端点，如下图右上角$\left[\begin{array}{c}5\\ 6\\ 1\end{array}\right]+\left[\begin{array}{c}3\\ -1\\ 0\end{array}\right]=\left[\begin{array}{c}8\\ 5\\ 1\end{array}\right]$；
3. 向量与向量运算，运算的结果是向量，含义是将两向量首尾相连，没有连起的另一首和尾组成的新向量，如下图中部$\left[\begin{array}{c}3\\ -1\\ 0\end{array}\right]+\left[\begin{array}{c}1\\ 2\\ 0\end{array}\right]=\left[\begin{array}{c}4\\ 1\\ 0\end{array}\right]$；
4. 点加上点？我们发现相加后额外的维度值变成了2，为了让额外的维度值保持为1，人为约定下，我们约定$\left[\begin{array}{c}x\\ y\\ w\end{array}\right]$代表的是$\left[\begin{array}{c}x/w\\ y/w\\ 1\end{array}\right]$。根据这个约定，两点相加得到的是两者的中点。

有了齐次坐标，我们就可以把几个基本的变换都用一个矩阵表示：

• 缩放 （Scale） ：$S(s_x,s_y)=\left[\begin{array}{ccc}{s}_x& 0& 0\\ 0& s_y& 0\\ 0& 0& 1\end{array}\right]$；
• （绕原点）旋转 （Rotate） ：$R(\alpha )=\left[\begin{array}{ccc}\cos \alpha & -\sin \alpha & 0\\ \sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right]$，一种简单的方法是代入特殊点推出矩阵各项的值。另外，可以发现这是一个正交矩阵；
• 平移 （Translate） ：$T(t_x,t_y)=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]$。
• 切变（Shear）：$x$方向上为$\left[\begin{array}{ccc}1& k& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$，$y$方向上为$\left[\begin{array}{ccc}1& 0& 0\\ k& 1& 0\\ 0& 0& 1\end{array}\right]$；
• 镜像（Mirror）：$x$方向上为$\left[\begin{array}{ccc}1& 0& 0\\ 0& -1& 0\\ 0& 0& 1\end{array}\right]$，$y$方向上为$\left[\begin{array}{ccc}-1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$。

线性变换加上平移变换合称为仿射变换（affine transformation）。具体来说，线性变换使得我们能够计算类似的表达式：$x^{\prime }=ax+by+cz$，仿射将其拓展至$x^{\prime }=ax+by+cz+d$。

同时复杂的变换可以分解为若干小变换依次完成，问题规约为矩阵分解、求逆、乘法等。举个例子，绕点c旋转，可以先把对象平移到原点$T(-c)$，然后旋转$R(\alpha )$，再还原回去$T(c)$，整个变换矩阵$E=T(c)R(\alpha )T(-c)$。

三维变换

Rodrigues' Rotation Formula：绕轴$n$旋转$\alpha$角度：

$$R(n,\alpha )=cos(\alpha )I+(1-cos(\alpha ))n{n}^T+sin(\alpha )\left[\begin{array}{ccc}0& -n_z& n_y\\ n_z& 0& -n_x\\ -n_y& n_x& 0\end{array}\right]$$

坐标系变换

视图变换（View transformation）

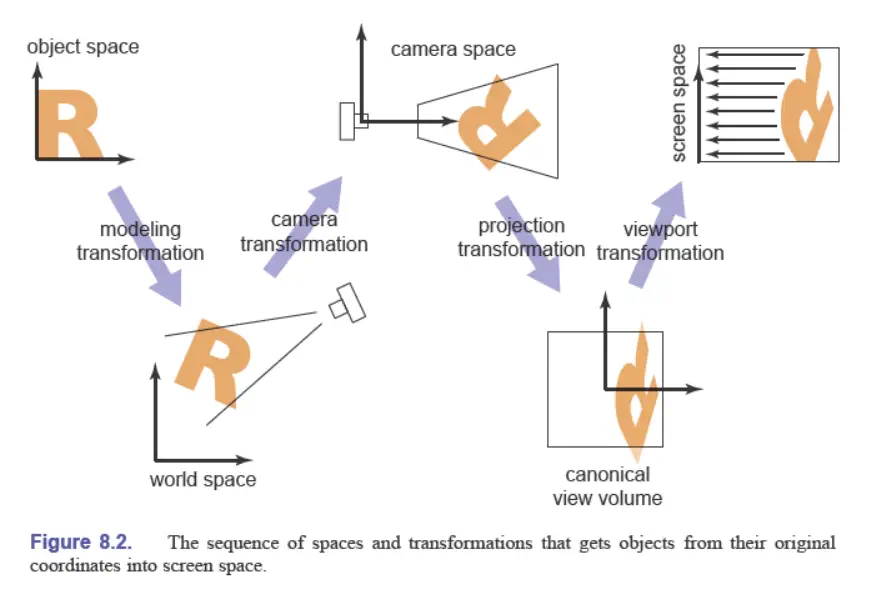
可以类比拍照：

1. 找到一个好的位置放置目标：几何变换；
2. 找一个好的角度来放置相机：视图变换；
3. 拍照：投影变换。

视图变换（View/Camera transformation）

如何定义相机位置：

• Position：$\overrightarrow{e}$；
• Look at/gaze direction: $\mathbf{g}$；
• Up direction：$\mathbf{t}$，可以想象手机横屏到竖屏的旋转，通过定义一个“向上”方向，消除这个角度的未知。

由于相机和物体一起运动，不会改变相机视角下的物体图像。因此不管相机怎么运动，总是可以通过移动物体得到相同的图像。为了简化表达，可以约定相机总是处于原点的位置，“up direction”向上的方向是 y，“look at”向右的方向 -z。

为了将相机移动到原点，我们需要做一个变换${\mathbf{M}}_{\mathbf{view}}$，囊括了：

1. 将$\overrightarrow{e}$移动到原点：$T_{view}=\left[\begin{array}{cccc}1& 0& 0& -x_e\\ 0& 1& 0& -y_e\\ 0& 0& 1& -z_e\\ 0& 0& 0& 1\end{array}\right]$；
2. 将$\mathbf{g}$旋转为$-z$方向；
3. 将$\mathbf{t}$旋转为$y$方向；
4. 将$\mathbf{g}\times \mathbf{t}$旋转到$x$方向。

后三个存在技巧，我们要将任意向量旋转到x、y或z上并不容易，但是如果反过来，将x、y或z方向上的单位向量旋转到其他向量的矩阵很容易写出来（考虑谁乘上单位向量得到目标向量即可），而旋转矩阵是正交矩阵，有$R^{-1}=R^T$，因此：

$$\begin{array}{rl}{R}_{view}& =(R_{view}^{-1}{)}^T\\ & ={\left[\begin{array}{cccc}{x}_{g\times t}& x_t& x_{-g}& 0\\ y_{g\times t}& y_t& y_{-g}& 0\\ z_{g\times t}& z_t& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]}^T\\ & =\left[\begin{array}{cccc}{x}_{g\times t}& y_{g\times t}& z_{g\times t}& 0\\ x_t& y_t& z_t& 0\\ x_{-g}& y_{-g}& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]\end{array}$$

投影变换（Projection transformation）

正交投影（Orthographic projection）

想象平行光源，或者无穷远处的点光源

惯用的做法，考虑任意长方体（orthographic view volumn），将其变换到标准视图大小（canonical view volumn），先平移，后缩放：

$$M_{ortho}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right]$$

TIP

这一步做完之后长方体会被拉伸，不过，最终会通过一次视口变换（viewport transformation）来还原物体的形状。更准确的说，视口变换将裁剪空间（三维归一化设备坐标空间，canonical）坐标转换为屏幕坐标，这一过程深度保持不彼岸，因为我们在应用视口变换之前，一般已经用透视投影处理过深度变化了：

$$M_{vp}=\left[\begin{array}{cccc}\frac{n_x}{2}& 0& 0& \frac{n_x-1}{2}\\ 0& \frac{n_x}{2}& 0& \frac{n_y-1}{2}\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

其中，$n_x$和$n_y$分别是屏幕视口的宽高，这个矩阵也是平移+缩放的结果。

透视投影（Perspective projection）

想象点光源

也可以分两步理解：保持near不变，先“挤压”视椎体成为立方体，再做一个透视投影：

根据相似三角形，$y_s=\frac{d}{z}y$，$x$方向也类似，从而这个变换应导致$\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)$ 变为 $\left(\begin{array}{c}dx/z\\ dy/z\\ \text{unknown}\\ 1\end{array}\right)$ 也即 $\left(\begin{array}{c}dx\\ dy\\ \text{still unknown}\\ z\end{array}\right)$，故

$$M_{persp\to ortho}=\left[\begin{array}{cccc}d& 0& 0& 0\\ 0& d& 0& 0\\ ?& ?& ?& ?\\ 0& 0& 1& 0\end{array}\right]$$

未知的那行怎么求呢？观察整个挤压过程，有两个现象：

1. near平面上的点在变换前后始终不变 -> near上点的z坐标记作$n$，变换后为$\left(\begin{array}{c}nx\\ ny\\ n^2\\ n\end{array}\right)$，那么空行应该符合$\left(\begin{array}{cccc}0& 0& A& B\end{array}\right)$的形式，即有$An+B=n^2$；
2. far平面上的点，其$z$坐标在变换前后始终不变 -> 考虑far的中心点，它在挤压前后都不变。中心点的x和y坐标都是0，z坐标记作$f$，则有$Af+B=f^2$。

现在，可以解出A和B的值：

$$M_{persp\to ortho}=\left[\begin{array}{cccc}d& 0& 0& 0\\ 0& d& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right]$$