微积分
MIT微积分公开课[1][2]学习笔记,课程总体偏向于应用,对理论部分没有太多深入。而且很多是高中内容,可适度跳着看。
导数
基本初等函数的导数
比较精彩的是指数函数和对数函数的部分。
令
INFO
当
令
的导数仍为 。 定义新函数对数函数
,若 ,则 。此时所有 可以表示为 ( )。 因此可以利用链式法则求 的导数: 而
则可以利用隐函数求导: 欲求
,其中 和 均是关于 的基本初等函数,利用隐函数求导法则: , 两边取对数 ,此时左右两边都是基本初等函数,有 ,当 时,即 ,其导函数为 。 欲求
,令 ,有: 如此提供了一种近似计算
的值的方法。
INFO
GS老爷子的微积分先导课程提到另一种定义指数函数的方法:
微积分本质是一种研究两个函数关系的科学。有这样一组关系
从
利用
线性近似
导数的定义,
由第三个式子可以进一步推出令
一个计算
有些时候,可能需要计算二阶近似来获得更接近的值,
INFO
二阶近似也可以给我们另一种视角来看待最大最小值问题(与导数、导数变化率的视角相对),
牛顿法
欲求
MVT
若
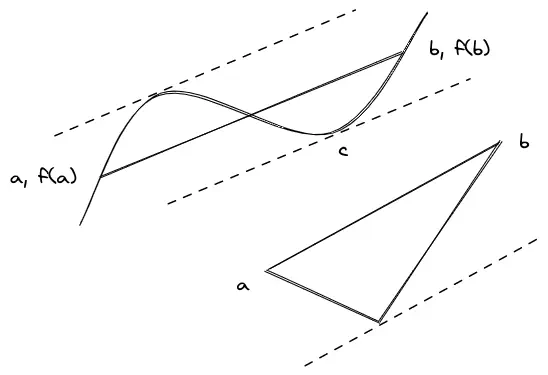
洛必达法则
对于
积分
FTC1
根据FTC1,若
举例来说,
FTC2
如果
INFO
FTC2还可以这样理解:
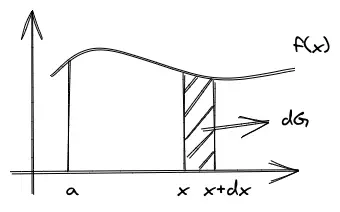
看图像理解证明比较简单,
FTC2使得我们拥有了一种新的定义函数的手段,例如定义函数
暂时忘掉以前学的对数函数的定义,利用这里定义的对数函数
另外一些积不出来但可以利用这种思想定义的函数如
分部积分法
由
反常积分
有时不好判断积分结果是否收敛,这时可以利用从洛必达法则中带来的思想,如果在
直线与平面
对非零点
直线除了可以看作是两个平面方程的交集之外,还可以用参数方程的方式定义:给定两个点
写成
INFO
对于以两平面交线方式给出的方程如
对于常见的
假设两不重合直线交于一点
INFO
如图,二元用切平面近似曲面,解出切平面方程可得
 :::
::: 开普勒第二定律
相同时间内行星扫过的面积相同,设半径为
Critical Points
由上面对切平面的讨论,如果
- 若
,则: - 若
,则取得局部最大值; - 若
取得局部最小值;
- 若
- 若
,鞍点; - 若
无法判断,可以代值进去。
同样可以利用线性近似的方法理解这个判别式,利用泰勒展开时,注意一阶线性近似由于
梯度向量
将
由于
WARNING
一直二维三维傻傻分不清楚的我:为什么
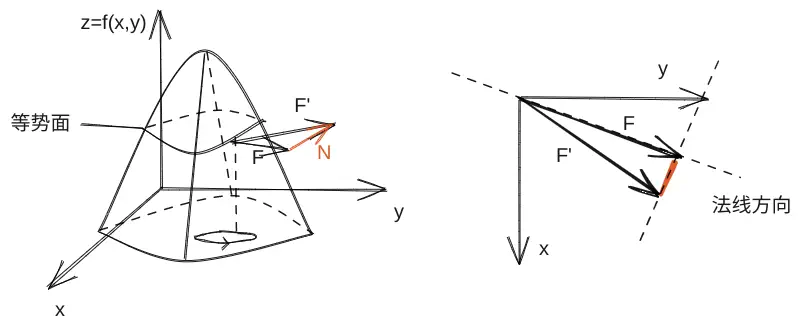
应用:求曲面上任一点的切平面
对于曲面方程
方向导数
用力的分解也许好理解一点。梯度给了我们对该点处曲线有多陡的直观感受,如果沿着梯度的方向,无论施加的力多大都无法实现在曲面上(等高线上)的移动(因为梯度向量与该处切平面垂直),而如果我们偏离一个角度,从而这个力在梯度方向上的分力不产生位移,带来加速度的是与梯度方向垂直方向的分力。用一个单位向量
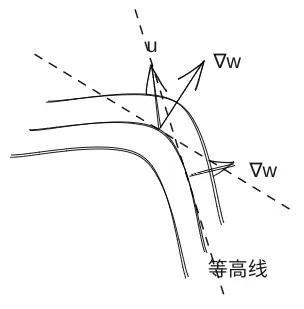
拉格朗日数乘法
在某些问题中,要求
非独立变量
另一种方法看待有
利用微分:
,为了消去 ,利用约束条件 ,有 ,从而 ,括号中的部分即 。 利用链式法则:
,同理由 可解出 ,带入第一个式子得到与微分法相同的结果。
WARNING
二重积分
雅可比矩阵
二重积分
依然利用微分:
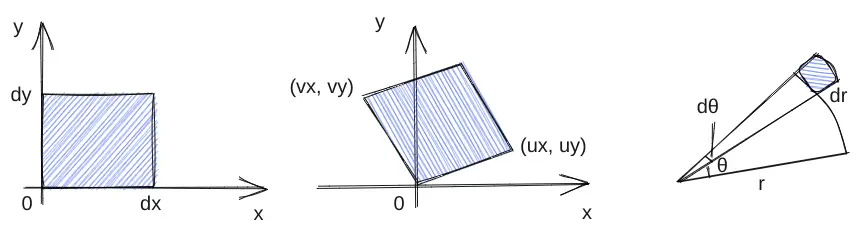
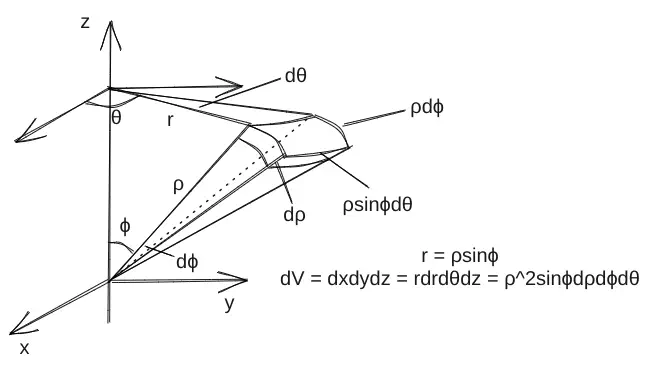
以极坐标系
向量场
做功与曲线积分
对一个小方向上的位移
INFO
力只有在位移的方向上才有功,所以是一个内积的关系。想想也是,如果力与位移方向垂直,这个力不做功。
为了求解,注意
由
Gradient Field
如果
INFO
由
在gradient field中,有对应的FTC:
当力使物体从
进一步推出有关gradient field的两个特性:
- 路径无关性:如果轨迹
、 具有相同的起点和终点,从而积分结果相同(做功相同); - 保守性:如果是闭合轨迹,则积分结果为
(先做正功,再做负功,或者反过来,总之最后啥也没干)。
物理意义
If the force field
如果向量场
Conservativeness means that energy comes from change in potential f, so no energy can be extracted from motion along a closed trajectory (conservativeness = conservation of energy: the change in kinetic energy equals the work of the force equals the change in potential energy).
仅对gradient field有四个等价的表述:
- 如果对任意闭合轨迹
有 ,则 是保守的; 是路径无关的(相同的终点相同做功,与路径无关); 是一个gradient field有 ; 是一个全微分(exact differential)形式。
通过令
旋度和散度
旋度
- 在平移运动中,
; - 在旋转变换中,
。
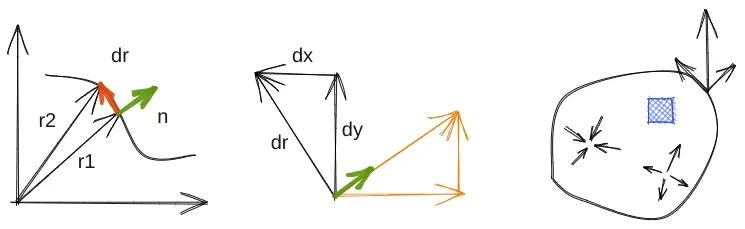
散度
INFO
一些个人理解:
如图,
在三维情况下,势
其实是一个“等势体”了。
从可汗学院盗的图:
格林公式
如果
或者写成:
可以用来将复杂的曲线积分简化为简单的二重积分或反之。例如拿它来证明gradient field的性质:
定理:如果
由
证明
- 定理其实可以分成两个部分
和 ; - 首先观察到如下事实,如右上角图所示,如果将
划分成 两个部分,两个部分的包裹曲线分别为 和 ,有 ,这是因为中间的那段各自方向相反,相互抵消了。
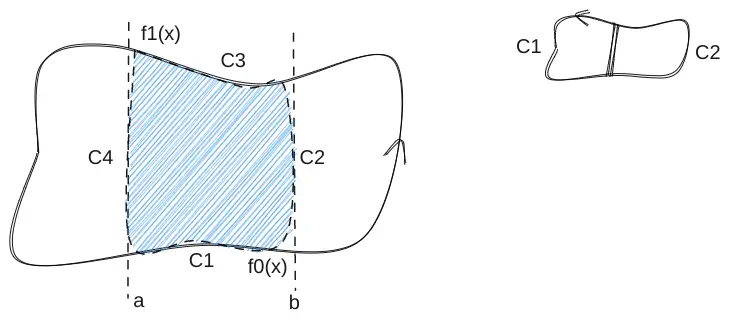
从而我们可以在
式中
由于所有的区域都可以被划分为这样一个个小的区域,将它们相加在一起后,左边就是外围曲线
除了告诉我们曲线积分可以转化为曲面积分,反过来格林公式也告诉我们区域面积可以用曲线积分求得
单连通区域
讨论来源于对
但也不是完全没有办法,我们可以把没有定义的这块挖掉,如下图,则有
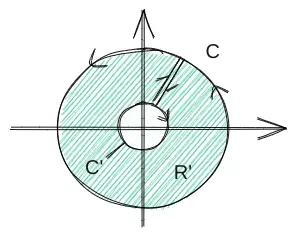
直观点说单连通区域就是个中间没有洞的区域,上面的图像看起来中间有个大洞,但如果将轨迹作为区域边界的话,它无疑是没有洞的。
三重积分
和二重积分基本类似,